Es la ecuación de estado del gas ideal, un gas hipotético formado por partículas puntuales sin atracción ni repulsión entre ellas y cuyos choques son perfectamente elásticos (conservación de momento y energía cinética). La energía cinética es directamente proporcional a la temperatura en un gas ideal. Los gases reales que más se aproximan al comportamiento del gas ideal son los gases monoatómicos en condiciones de baja presión y alta temperatura.
En 1648, el químico Jan Baptist van Heltmont creó el vocablo gas, a partir del término griego kaos (desorden) para definir las génesis características del anhídrido carbónico. Esta denominación se extendió luego a todos los cuerpos gaseosos y se utiliza para designar uno de los estados de la materia.
La presión ejercida por una fuerza física es inversamente proporcional al volumen de una masa gaseosa, siempre y cuando su temperatura se mantenga constante. o en términos más sencillos:
A temperatura constante, el volumen de una masa fija de gas es inversamente proporcional a la presión que este ejerce. Matemáticamente se puede expresar así:
donde k es constante si la temperatura y la masa del gas permanecen constantes.
Cuando aumenta la presión, el volumen baja, mientras que si la presión disminuye el volumen aumenta. No es necesario conocer el valor exacto de la constante k para poder hacer uso de la ley: si consideramos las dos situaciones de la figura, manteniendo constante la cantidad de gas y la temperatura, deberá cumplirse la relación:
Las primeras leyes de los gases fueron desarrollados desde finales del siglo XVII, aparentemente de manera independiente por August Krönig en 1856 y Rudolf Clausius en 1857. La constante universal de los gases se descubrió y se introdujo por primera vez en la ley de los gases ideales en lugar de un gran número de constantes de gases específicas descriptas por Dmitri Mendeleev en 1874.
Ecuación General De Los Gases Ideales
Partiendo de la ecuación de estado:
Tenemos que:
Donde R es la constante universal de los gases ideales, luego para dos estados del mismo gas, 1 y 2:
Para una misma masa gaseosa (por tanto, el número de moles «n» es constante), podemos afirmar que existe una constante directamente proporcional a la presión y volumen del gas, e inversamente proporcional a su temperatura.
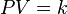
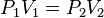
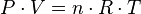
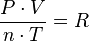


No hay comentarios:
Publicar un comentario